A Problem too Simple to Solve

In the bleary backstreets of mathematical mysteries, where numbers lurk like a menacing penumbra, the Collatz Conjecture reigns as an enigmatic crime lord, untouchable since 1937. Crafted by the cunning mind of Lothar Collatz, this puzzle's a sly fox in the mathematical henhouse. It goes like this: grab any number, if it's playing it straight and even, cut it down to size--halve it (x / 2). But if it's playing odd, give it the old one-two: triple it and add one for good measure (3x + 1). Do this little dance with each fresh result, and they all end up at the same dead-end street – the big one, numero uno. From there, it will do the only pirouette ever discovered in a Collatz sequence, to an eternal beat of 4-2-1, 4-2-1.

It's a riddle wrapped in a conundrum, cloaked in an enigma. It's had the best mathematical gumshoes on the beat--guys with brains that could give Paul Erdős a run for his money. Erdős himself once tipped his hat to the problem, famously saying that "mathematics is not yet ready for such problems." Simple enough for a schoolyard kid to get the gist, yet it's got the seasoned number crunchers pulling out their hair. It’s the kind of problem that lights up a smoke and laughs in the face of computational brute force.

Computers have been thrown into the fray, churning through digits bigger than my bar tab, but the answer's always just out of reach, like the shadow of a suspect turning the corner. This caper’s drawn lines through chaos theory, algorithmic alleyways, and more, but still, the Collatz Conjecture remains at large, a smooth criminal slipping through the fingers of justice. It’s a stark reminder in this town of numbers and logic that some mysteries don’t play by the rules, and they don’t go down easy.

***

Part of the complexity of the research is purely computational. We have checked at least every number less than or equal to 2⁶⁸, or 295,147,905,179,352,825,856. Even that relatively-modest effort likely took years to accomplish. No exceptions to the Collatz Conjecture were found in that range.

What we've thus far settled for is investigation into the properties of numbers that seem to yield sequence lengths that are statistically unusual. A simple function, written in Python, to create a Collatz sequence and report its length for integer n would look like this:

def collatz_sequence_length(n):
    length = 0
    while n != 1:
        if n % 2 == 0:
            n = n // 2
        else:
            n = 3 * n + 1
        length += 1
    return length

We can think of this sequence length as the number of stops in a flightpath before a number under test eventually lands on 1. If the above while loop were to suddenly run forever, we'd know the system had either run out of memory (likely), or that we've stumbled on a number that does not obey the conjecture (sadly unlikely).

Let's try to find some unusually long flights in a range of a size we can manage with just a laptop--say 5 - 2¹⁸:

max_range = 2**18  # 262144
longest_sequence = 0
number_with_longest_sequence = None

for i in range(1, max_range + 1):
    current_sequence_length = collatz_sequence_length(i)
    if current_sequence_length > longest_sequence:
        longest_sequence = current_sequence_length
        number_with_longest_sequence = i

number_with_longest_sequence, longest_sequence

// 230631, 442

Ok, we've identified a number with a flight length of 442 steps. That does seem like a lot. To contextualise this number, we need to know how it compares to the mean for numbers of a similar size, say 100000 to 300000:

def mean_collatz_sequence_length(start, end):
    total_length = 0
    for n in range(start, end + 1):
        length = 1
        while n != 1:
            n = n // 2 if n % 2 == 0 else 3 * n + 1
            length += 1
        total_length += length
    mean_length = total_length / (end - start + 1)
    return mean_length

mean_length = mean_collatz_sequence_length(100000, 300000)
mean_length

// 125.57944210278949

Great--that does seem like a significant distance from the mean. Let's calculate the number of standard deviations from the mean 442 represents:

def collatz_sequence_variance(start, end, mean):
    sum_of_squares = 0
    for n in range(start, end + 1):
        length = 1
        while n != 1:
            n = n // 2 if n % 2 == 0 else 3 * n + 1
            length += 1
        sum_of_squares += (length - mean) ** 2
    variance = sum_of_squares / (end - start + 1)
    return variance

# Calculate the variance of the Collatz sequence lengths for numbers from 100000 to 300000
mean_length = 125.57944210278949  # Reusing the mean calculated previously
variance = collatz_sequence_variance(100000, 300000, mean_length)

# Calculate the standard deviation
std_deviation = variance ** 0.5

# Calculate how many standard deviations above the mean is a sequence length of 442
distance_from_mean = (442 - mean_length) / std_deviation

distance_from_mean

// 5.833275544016192

Many are more accustomed to thinking about rarity in terms of percentile. For example, I am in the 99th percentile for wasting time on unsolvable problems, and hopefully you are in the 99th percentile for willingness to read about them. Let's use a cumulative distribution function to further marvel at the rarity of an event 5.83 standard deviations above the mean:

from scipy.stats import norm

percentile = norm.cdf(5.833275544016192) * 100

percentile

// 99.99999972825148

Wow, the 99.99999973rd percentile! Still unconvinced this number is special? Many people like to use phrases like, "you're one in a million." That's sweet. Let's calculate the inverse of the percentile to evaluate the rarity of this sequence in those terms:

one_out_of = 1 / (1 - percentile / 100)

one_out_of

// 367987279.7264082

You're doing a heck of a job, 230,631. You're one in 367,987,280! I think we've made our point.

So what makes 230,631 so special, and could it help us find other numbers that generate long flight times? It's not immediately clear. I'll spare you my work, but it isn't part of the Fibonacci sequence. It isn't a Pell number. It isn't a Lucas number. It isn't a Catalan number. It isn't a happy number (yes, that is a real thing). It's neither a perfect number, nor is it an abundant number--it's deficient. It's certainly neither a square nor a cube. It is a palindrome if we represent it in balanced ternary (base-3), but I think we're reaching at this point. It's seemingly unremarkable, except that it happens to produce a Collatz sequence length that is a statistical outlier. As we don't understand what makes it special, we'd be hard-pressed to use it to help us identify other statistical outliers, with the goal of eventually finding a number producing an infinite loop.

Failing that, let's have a look at the flightpath itself, to identify its greatest ascents and deepest dives:

import matplotlib.pyplot as plt

def collatz_sequence(n):
    sequence = [n]
    while n != 1:
        if n % 2 == 0:
            n = n // 2
        else:
            n = 3 * n + 1
        sequence.append(n)
    return sequence

collatz_seq = collatz_sequence(230631)

fig, ax = plt.subplots(figsize=(10, 6))
ax.set_title('Collatz Sequence Flight for 230631')

x_coords = list(range(len(collatz_seq)))

ax.plot(x_coords, collatz_seq, color='coral', linewidth=0.5)
ax.set_xlabel('Steps')
ax.set_ylabel('Value')

plt.show()

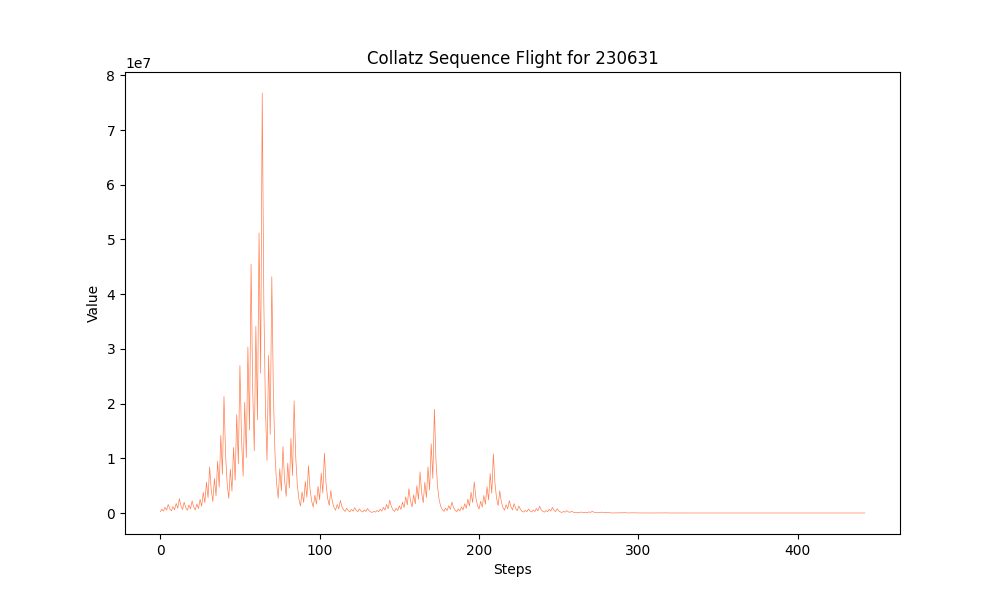
We came within a stone's throw of 100,000,000 early in the sequence! That's pretty cool. But what we're truly trying to identify are large near-loops. To better view those, we can try viewing the flight in 3D, from the perspective of the Z-axis:

from mayavi import mlab
import numpy as np

def collatz_sequence(n):
    sequence = [n]
    while n != 1:
        if n % 2 == 0:
            n = n // 2
        else:
            n = 3 * n + 1
        sequence.append(n)
    return sequence

collatz_seq = collatz_sequence(230631)

x, y, z = 0, 0, 0
angle_xy, angle_z = 0, 0
scale = 0.1

points_x, points_y, points_z = [x], [y], [z]

for value in collatz_seq:
    # Change angles based on odd or even value
    if value % 2 == 0:
        angle_xy += 45
        angle_z += 10
    else:
        angle_xy -= 45
        angle_z -= 10

    x += scale * np.cos(np.radians(angle_xy))
    y += scale * np.sin(np.radians(angle_xy))
    z += scale * np.sin(np.radians(angle_z))

    points_x.append(x)
    points_y.append(y)
    points_z.append(z)

mlab.figure(bgcolor=(1, 1, 1))
mlab.plot3d(points_x, points_y, points_z, color=(0.9, 0.4, 0.4), tube_radius=0.005)
mlab.show()

Here's what's going on:

• The Y-axis represents the value of the number at each step.
• The X-axis changes direction based on whether the number is even or odd.
• The Z-axis shows progress in the sequence over time.

And here's the resulting marvel in Mayavi:

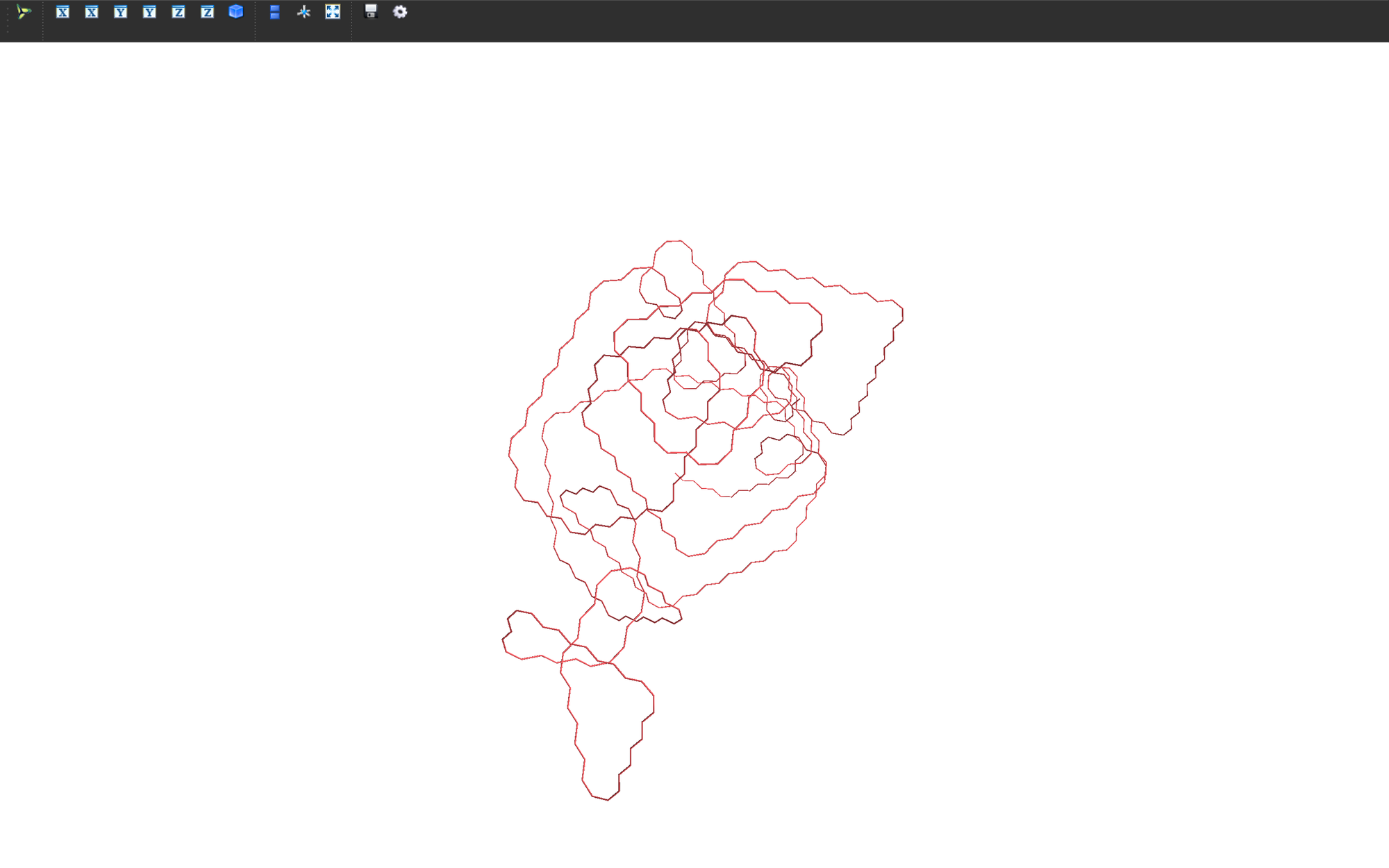
Gorgeous. Is that South America at the bottom?

So what did we learn? I would estimate roughly nothing, other than a healthy appreciation for how easy it is to waste time banging one's head against this enticingly simple puzzle. It's infuriating to realise that, despite centuries of study, integers still hold many mysteries, particularly in the context of non-linear operations like those in the Collatz sequence.

The Collatz Conjecture, with its stark simplicity, stands as a defiant enigma in the face of established number theory and dynamical systems. These fields, steeped in complex theories and intricate methodologies, seem ill-equipped to unravel the conjecture's deceptively straightforward rule. It's as if the conjecture exists in a different mathematical universe, where the conventional tools and approaches of these disciplines lose their potency, leaving the conjecture to hover just beyond the realm of current understanding.

This may be one puzzle that is too simple to be solved.